​Na geometria plana temos dimensão de 2 D, suas figuras são planificadas e não tem volume.

• Área de algumas figuras planas:

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

• ​PITÁGORAS

O velho tio pit, a fórmula básica c²= a²+b².

​

​

  Tio pit no quadrado:



​



















































Tio pit no triângulo:

























​



​

​













Exemplo:

O perímetro de um triângulo equilátero é 18 cm. Calcule a área desse triângulo.



​



















Agora temos duas maneiras de descobrir a altura para calcular a área:
 

1ª) Fórmula: h = l √3/2
h = 6√3/2 → h = 3√3
 

2ª) c² = a² + b²:
6² = h² + 3² (é 3 porque é 6/2)
36 = h² + 9²
27 = h²  → h = √27
h = 3√3
é claro que a 1ª maneira é mais fácil e ocupa menos linhas :D
 

Calcular a área:
 

A = b x h/2  → A = 6 x 3√3 /2  → A= 9√3 cm²

​

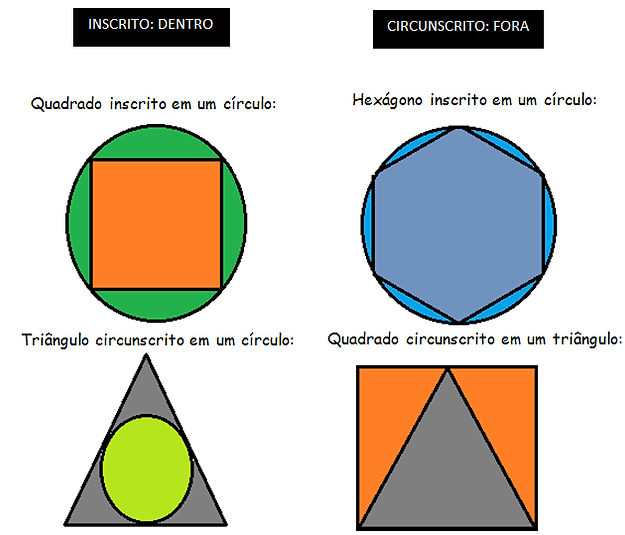
• Polígonos inscritos e circunscritos:

​



































​

​

Para calcular figuras circunscritas e inscritas temos um formulário lógico:
• Quando temos um hexágono inscrito em um círculo o raio é igual ao lado do mesmo.
• Quando temos um triângulo inscrito em uma circunferência a altura dele é h=3r/2
• Quando temos um quadrado inscrito em um circulo a diagonal dele é 2r.
• Quando temos um circulo inscrito em um quadrado o lado é igual a 2r.
 

E tem muitas outras coisas que vamos percebendo ao decorrer dos exemplos:
 

1) Calcule a área de um circulo inscrito em um quadrado de lado 6cm.

​





















​

• Exemplos bacanas:

Numa circunferência de raio r e centro O é fixado um diâmetro BC e uma corda AB de comprimento igual ao raio r. Calcule, em função de r, a área do triângulo OAB.

​















O ponto O é o ponto de vértice do triângulo então nele tem um ângulo, os segmentos BO e AO são os lados, então eles são iguais ao raio e o segmento BA é a base, que irei chamar de x. Representação:













1pi= α → pi rad= 180⁰

3,14rad= 180⁰
rad = 180⁰/3,14 = 57,3⁰ (valor aproximado)

​

Depois temos que dividir o ângulo por  2 pois usaremos só a metade do triângulo equilátero. Então: 53,3º/2= 28,6º

Temos que descobrir o valor de "x", "r" e "h" então temos que utilizar o seno e o cosseno para descobrir (pois temos o ângulo e tals).

​

sen 28,6º=x/r  // como não sabemos o valor do seno e 28,6º podemos utilizar o valor de seno do ângulo mais próximo, que no caso é o de 30º que é 0,5.

 

0,5=x/r  -> 0,5r=x



cos 28,6º= h/r -> 0,86r=h

​

A= b x h/2 -> 2*0,5r*0,86r/2

A= 0,86r²/2



A(r)= 0,43r²



2) Determine a área do terreno abaixo usando as medidas dadas.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

Tínhamos a figura do terreno, então ele foi divido em 3 figuras geométricas (um triângulo, um retângulo e um trapézio), agora fica mais fácil de calcular a área do terreno :D
Aretângulo= 12*6 = 72m²
Aretângulo=5*6/2 = 15m²
Atrapézio= ((8+3)*4)/2 = 22m²
Atotal= 72m²+15m²+22m²= 109m²



3) Qual a área de toda a parte colorida da figura abaixo? Qual é a área da região não colorida?









​
 

​

​

​

​

Temos 4 partes coloridas e elas formam triângulos então é só calcular a área do triângulo e multiplicar a área por 4 para saber a área da parte colorida :D
 

​

​

​

​

​

​

​

​

​

Atriangulo = 2*2/2= 2 cm²  → 2*4= 8 cm² é o valor da área colorida.
 

Para calcular a parte não colorida temos que descobrir o lado do triângulo (que na figura acima eu chamei de x), então temos que utilizar o tio pit ;)
 

x² = 2² + 2²
x² = 8 → x=√8
x = 2√2
Aquadrado= L² (no caso x²) então, Aquadrado = (2√2)²
Aquadrado= 8 cm²